Integrals

This page explains the strategy and mathematical derivations for spectra processing. It discusses the thinking behind routines, and not the routines and algorithms used themselves.

Background correction

Below figure shows a peak in green and two backgrounds left and right surrounding the peak.

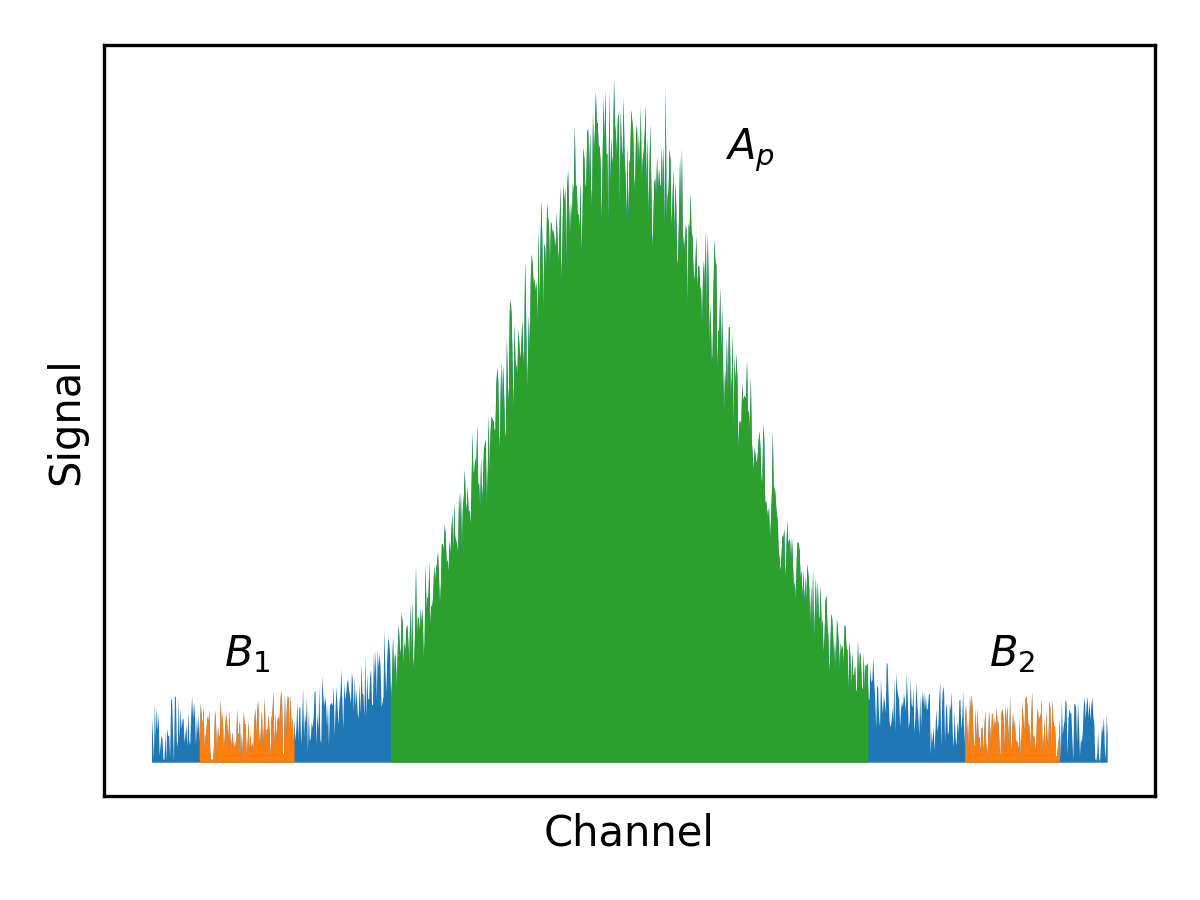
Let us define \(A_{p}\) as the peak area (green) and \(B_{1}\) and \(B_{2}\) as two backgrounds, left and right, respectively. Furthermore, let us generalize the backgrounds as \(B_{i}\), where \(i\) represents any background. In above example, \(i \in \{1,2\}\). Furthermore, let’s define the number of channels in the peak as \(n_{p}\) and the channels in background \(i\) as \(n_{i}\).

Without background corrections and using counting statistics, we can write the total area under the peak and its uncertainty as \(A_{p} \pm \sqrt{A_{p}}\). With background correction, let us define the peak area as \(A_\mathrm{corr}\) and its uncertainty as \(\sigma_{A_\mathrm{corr}}\).

To perform a background subtraction, we first have to define the channel normalized background, i.e., the amount of background that is present per channel. This can be written as:

\[B_{\mathrm{ch},i} = \frac{B_i}{n_i}\]

From this, we can derive the average background by averaging over all \(i\), such that:

\[B_\mathrm{ch} = \frac{1}{N} \sum_{i=1}^{N} \frac{B_i}{n_i}\]

Its uncertainty, based on counting statistics, is defined as:

\[\sigma_{B_\mathrm{ch}} = \frac{1}{N} \sum_{i=1}^{N} \frac{\sqrt{B_i}}{n_i}\]

Here, we assume that the number of channels is known without any uncertainty. This is generally true when dealing with mass spectra.

From this formalism, we can now calculate the background corrected peak as:

\[\begin{split}A_\mathrm{corr} &= A_p - n_p \cdot B_\mathrm{ch} \\ &= A_p - \frac{n_p}{N} \sum_{i=1}^{N} \frac{B_i}{n_i}\end{split}\]

Propagating the uncertainties, we can calculate the uncertainty of the background corrected peak as:

\[\sigma_{A_\mathrm{corr}} = \left[ \left(\sqrt{A_p}\right)^2 + \left( \frac{n_p}{N} \sum_{i=1}^{N} \frac{\sqrt{B_i}}{n_i} \right)^2 \right]^{1/2}\]